Necessity and Sufficiency

Argument and Information

In the previous essay in this series, we introduced the idea of relevance, and said that a premise is relevant to the conclusion iff $P(A|B)>P(A|\overline{B})$.

Consider the argument (𝐴) this is a good candidate for the job because (𝐵) he has a pulse. Having a pulse may not be a very persuasive reason to hire somebody, but it is probably quite relevant, because if the candidate did not have a pulse, the subject would probably be much less likely to want to hire him. That is $P(A|B)>P(A|\overline{B})$.

So to be persuasive, the premise must not only be relevant: it must actually change the probability that the subject accepts the conclusion.

Why isn’t 𝐵 he has a pulse persuasive to the subject? Because presumably, he has a pulse does not tell the subject anything he didn’t already know, or at least didn’t already assume was probably true. An argument can only change the beliefs of a Bayesian reasoner if it provides new information.

Necessity and Sufficiency

So the effect of learning that the premise is true or false depends on the subject’s prior degree of acceptance of the premise.

If the subject already accepts the premise and conclusion, and they wouldn’t accept the conclusion if they didn’t accept the premise, then the premise is necessary. If the subject does not already accept the premise or the conclusion, but they would accept the conclusion if they did accept the premise, then the premise is sufficient.

Now, a Bayesian agent may only partially accept the premise or conclusion. And yet their partial acceptance of the premise may be necessary for their partial acceptance of the conclusion. For example, the subject may believe that the candidate almost definitely has a pulse, and that they are probably a good candidate, but almost definitely would not be if they didn’t have a pulse. So necessity is a matter of degree.

In fact, a premise can be just a little bit sufficient/necessary. The belief that Tom Cruise is in Top Gun II might be necessary for the subject’s belief that Top Gun II is a little more likely than average to be a good movie. And learning that Tim liked Top Gun II may be sufficient to conclude that it may be worth going to see.

This contrasts with traditional logical ideas about necessity and sufficiency, where because propositions are either true or false, things are either necessary/sufficient or not.

In the rest of this section, we will quantify necessity and sufficiency and demonstrate the following relationships between them:

• The greater the prior acceptance of the premise, the more necessary
• The greater the prior acceptance of the premise, the less sufficient
• The more necessary the premise for the conclusion, the more sufficient the rejection of the premise for rejection of the conclusion, and vice versa.

Examples of Sufficiency and Necessity

Necessary but not Sufficient:

Consider the following examples. You probably agree that these premises all seem like they should be necessary but not sufficient.

• This is a good candidate because he has a pulse.
• Tweety can fly because he has wings.
• My car will start because it has a battery.

Notice also that these premises all seem, a priori, probable. So if the subject learned that these premises were not true, this would probably be sufficient to reject the premise.

Sufficient but not Necessary:

For the following examples, you probably agree that the premises all seem like they should be (fairly) sufficient for the conclusion, but not necessary.

• This is not a good candidate because he doesn’t have a pulse.
• John can fly because John is a bird.
• The world will end next year because it will be hit by a giant asteroid.

Notice also that these premises all seem, a priori, improbable. So if the subject learned that premises were true, this would be probably sufficient to accept the premise.

Both Sufficient and Necessary:

For the following examples, you probably agree that the premises seem like they are both somewhat sufficient and somewhat necessary. But notice also that these premises all seem, a priori, neither very probable nor very improbable.

• This is an above-average candidate because she scored above average on the skills test.
• It is nighttime because it is dark outside.
• The economy is doing poorly because stock prices are falling.

Now what if the subject learned that these premises were definitely true, or definitely false? This would probably be almost sufficient to accept or reject the premise, respectively.

Quantifying Necessity and Sufficiency

We can quantify the degree to which a premise is necessary by considering how much the subject’s belief in the conclusion would decrease if they rejected the premise. Likewise we can quantify sufficiency as how much their belief in the conclusion would increase if they accepted the premise. These difference can be measured as an absolute difference, percent difference, etc. We will focus on the absolute difference.

Necessity

The necessity of 𝐵 to 𝐴 is:

Sufficiency

The sufficiency of 𝐵 to 𝐴 is:

Identities

Necessity = Relevance × Acceptance

Clearly, a premise must be relevant to be either necessary or sufficient.

Further, for a premise to be necessary, the subject must to some degree accept it (otherwise learning it was false it would not be new information).

In fact, necessity is just the product of relevance and acceptance of the premise (proof).

Sufficiency = Relevance × Rejection

And for a premise to be sufficient, the subject must not completely accept it (otherwise, learning it was true would not be new information). In fact, sufficiency is just the product of relevance and rejection of the premise (proof):

Necessity + Sufficiency = Relevance

It follows that as long as the premise is not completely accepted or rejected, it is both necessary and sufficient.

What’s more, a premise cannot be relevant if it is completely accepted or rejected. For example, if the subject completely accepted or rejected the premise ($P(B)$ equals 0 or 1), relevance would be undefined, because either $P(A|B)$ or $P(A|\overline{B})$ would be undefined. For example, if $P(B)=0$, then $P(A|B)=P(A,B)/P(B)=P(A,B)/0$, which is undefined.

This means that as long as the premise is relevant, it will be both necessary and sufficient to some degree. In fact, relevance is the sum of necessity and sufficiency. So $P(B)$ just partitions relevance into components of necessity and sufficiency. The more the premise is accepted, the more necessary and the less sufficient, and vice versa.

This relationship is illustrated in the chart below:

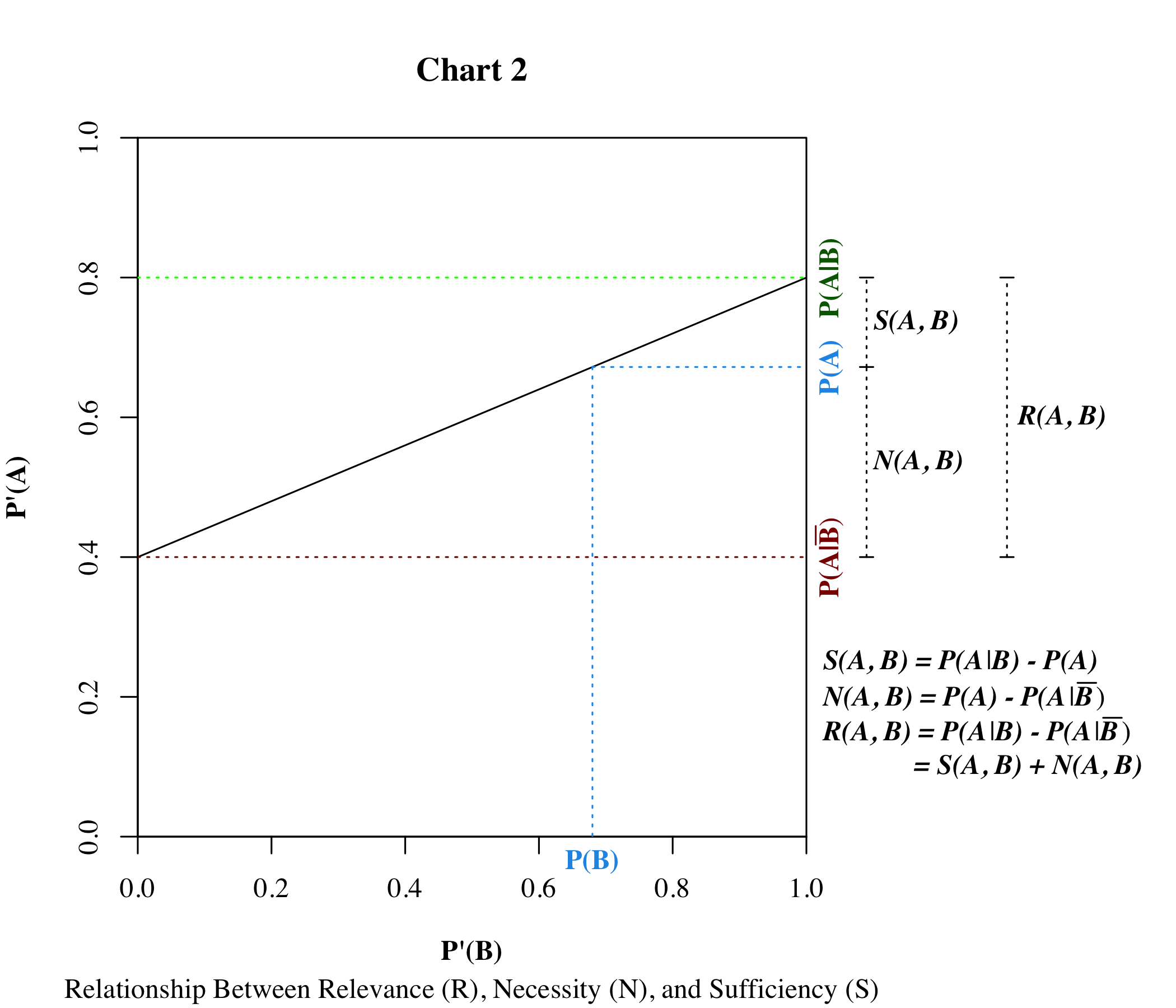
So when we say that he has a pulse is necessary but not sufficient, we mean that it is very necessary, and not very sufficient. Likewise, he is the most qualified candidate ever may be quite sufficient, but certainly not very necessary.

Rejection of the Premise

To the degree that the premise is necessary for the conclusion, the rejection of the premise is sufficient for rejection of the conclusion. Thus he doesn’t have a pulse is sufficient for the conclusion this is not a good job candidate (proof).

It follows trivially that, to the degree that the premise is sufficient for the conclusion, rejection of the premise is necessary for rejection of the conclusion.

Next in this Series

So we have thoroughly explored the idea of necessity and sufficiency, and how they relate to relevance and the degree of acceptance of the premise.

But an important question remains. Will the subject accept the premise? In the next essay in this series, we explore this question and define the ideas of informativeness and persuasiveness.

Proofs

The proofs below use the following equality, which is derived in the previous essay.

Proof 1

Necessity = Relevance × Acceptance

Proof 2

Sufficiency = Relevance × Rejection

Proof:

Proof 3

Proof: